COMPOSITION
DE
Un corps peut être
divisé en fragments extrêmement petits : La
molécule
La molécule est
formée d’éléments encore plus petits : L’atome.
STRUCTURE
DES ATOMES
Un atome se
compose : d’un noyaux autour duquel gravitent
les électrons

Certains atomes
ont des électrons qui peuvent quitter leur orbite et passer ainsi d’un
atome à l’autre.
Ces électrons sont appelés : électrons libres
Un matériau
comportant des électrons libres est conducteur de l’électricité
On peut soit par
frottement ( électricité statique.), soit
par chimie ( pile, batterie), soit par
magnétisme ( alternateur, dynamo.) déplacer
les électrons libres d’un corps.
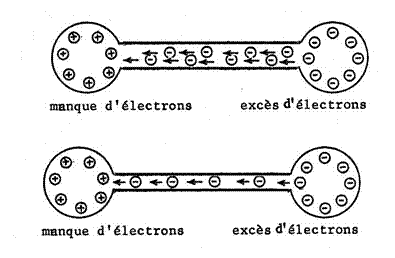
On aura donc des
corps plus ou moins chargés en électrons.

Cette différence
de charge est aussi appelée TENSION, symbole U
Elle se mesure en volts. (V) avec un voltmètre
branché entre les bornes
dont on veut mesurer
la différence de charge.

LE COURANT
ELECTRIQUE
Si on relie deux
corps de charges différentes par un fil conducteur, naturellement,
les électrons vont aller boucher les trous de l’autre côté.

Ce déplacement
d’électrons est appelé : courant électrique ou
Intensité, symbole I
Il se mesure en ampères (A)
à l’aide d’un ampèremètre
branché en série dans le circuit à étudier

OU avec une pince ampéremètrique
afin de ne pas couper le fil du montage

Selon que le fil
conducteur reliant les deux corps de charges différentes est de nature ou de
section variable, les électrons ne circuleront pas de
la même façon à l’intérieur des fils.
Gros fil =
gros passage Petit fil=
petit passage
On dit que les
conducteurs n’ont pas la même résistance au
passage du courant.
Cette résistance
se mesure en ohms., symbole W.
- Soit à l’aide d’un
ohmmètre placé aux bornes de la résistance à
mesurer celle-ci étant débranchée de sa source
d’alimentation

Nota : la
lampe étant débranchée, elle ne brille pas, donc elle
ne chauffe pas
C’est une mesure à froid
- MESURE DE
RESISTANCE à l’aide d’un voltmètre et d’un ampèremètre

En appliquant
ensuite la formule de
U =
R x I
Nota : en
branchant la lampe à son générateur, elle brille donc elle
chauffe
c’est une mesure à chaud
ASSOCIATION
DE RESISTANCES
- en SERIE -
Loi des
branches : U
= U1+U2+U3

NOTA : le
courant I est le même dans toute la branche
L’ensemble de ces
résistances peut être remplacé par une résistance
équivalente
en
série : R équivalente
= r1 + r2 + r3 etc…

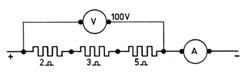
Calculez la
valeur de R équivalente, puis celle de I dans le circuit.
Exercice :
……………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………….
……………………………………………………………………………………………………………………………………………………….
- en PARALLELE -
U = U1 = U2

L’intensité du
courant principal est égale à la somme des courants dérivés

L’ensemble de ces
résistances peut être remplacé par une résistance
équivalente
en
paralléle : R équivalente
= (r1 x r2 ) / ( r1 + r2) S’il n’y a que
deux résistances dans le circuit

S’il y a plus
de deux résistances dans le circuit, la
formule devient : 1/R équiv
= 1/r1 + 1/r2 + 1/r3 etc…
Exercice :
Calculez la valeur de I dans chaque branche puis celle de R équivalente .

Exercice :
Trouvez les valeurs des résistances dont la valeur n’est pas indiquée sur le
dessin.

INFLUENCE DE
On
a vu que la résistance dépendait de la grosseur du fil – donc de sa section (S)
Mais
aussi de la longueur du fil (L), ainsi que de sa résistivité
(r)
R = r . L/S avec L en m avec r en W.m avec S en m²
Lors
de la mesure de la résistance d’une ampoule – à froid – et - à chaud – vous avez constaté que la résistance à chaud était environ 10
fois plus grande qu’à froid.
Or,
la chaleur n’a ni changé la section du filament,
ni augmenté la longueur du filament de
l’ampoule.
C’est donc la résistivité
du filament qui a augmenté.
La
formule de calcul d’une résistance en fonction de la température est :
Rt = R0 . (1 + a t)
avec Rt
(résistance à la température
« t »)en
W
avec R0 (résistance à la température
avec t (température) en Kévin ou en °C .
avec a
(cœfficient de température)en Kevin-1


Exercices :
-1- Le filament en
tungstène d’une lampe 24 V à incandescence mesure
Calculez la
section S du filament.
Calculez sa
résistance à zéro degrés Celsius
Calculez sa
résistance à
-2- L’enroulement d’un moteur (fil de cuivre)
a une résistance de 0,424 W à
Quelle est la température de
l’enroulement ?
FORCE –
TRAVAIL – PUISSANCE
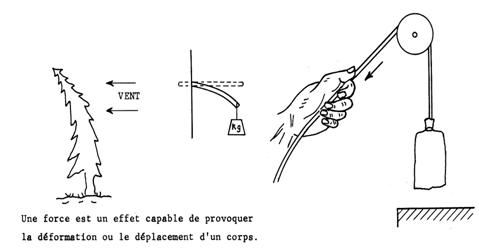
Notion de FORCE
Notion de TRAVAIL.

Notion de PUISSANCE

PUISSANCE
La puissance
(symbole P) d’une machine est le travail que peut fournir cette machine en 1 seconde
Elle se mesure en watts (W), mais comme cette unité est petite, nous
utiliserons souvent le kilo watt (KW)
Parfois, quelques
vieilles machines affichent encore leur puissance en cheval
vapeur (ch)

1 KW = 1000W
1 ch = 736W
Ordre de grandeur
de quelques puissances :
-
rasoir
électrique 10 w
-
ampoule
60 w
-
fer à
repasser 1500 w
-
Convecteur
de 500 à 3000w
-
Locomotive
6000 Kw
-
Turbine
de barrage 10 000 Kw
-
Centrale
atomique 1450 méga watts
La puissance
absorbée par un récepteur se mesure avec un wattmètre
qui donne
directement le résultat en watts .

Si vous êtes branchée
sur une alimentation de courant CONTINU ( exemple : pile, batterie)
ou si vous avez
comme récepteur une RESISTANCE ( exemple:four
électrique, lampe à incandescence, convecteur….)
La puissance
absorbée par un récepteur peut aussi se mesurer avec :
un voltmètre et un ampéremètre

En appliquant
ensuite la formule :
P = U x I
Autres formules
permettant de calculer P :
P = U²/R P = R x I²
Avec I en ampères
U en volts
R en ohms
EFFET JOULE
Dans leur
déplacement, les électrons qui se heurtent aux
atomes du conducteur dégagent de la chaleur
Un conducteur
parcouru par un courant dégage de la chaleur

L’énergie (symbole W ) dissipée sous
forme de chaleur s’appelle l’effet Joule
W = R . I². t
Elle s’exprime en Joules (J) si le temps –t- est en secondes
Elle s’exprime en watt heure (Wh) si le temps –t- est en heures
Puissance thermique (P) dissipée par effet Joule :
P = R . I²
La quantité de chaleur (Q) dégagée s’exprime en calories (cal) 1 Calorie, c’est la quantité
d’energie nécessaire pour élever la température d’un gramme d’eau de 1 degrés
Celsius
1 Cal = 4,18 Joules
Utilisation de l’effet Joule :
Chauffage
Eclairage
Fusibles
thermostats
Inconvénients de l’effet Joule :
Echauffement
des lignes, des machines
Diminution
des rendements des machines non thermiques
Risques
d’incendies
PUISSANCE EN
MONOPHASé

Puissance apparente (S)
Elle caractérise
le plus souvent les générateurs alternatifs
(alternateur, onduleur, transformateur…)
C’est
la puissance réelle que fournit EDF.
S = U . I
La puissance
apparente se mesure avec voltmètre et un
ampéremètre
PUISSANCE ACTIVE
(P)
C’est la puissance
qui est à l’origine du travail fournit par la
machine
P = U. I . Cosj
(exemple : ce
moteur va consommer une puissance active de 3Kw)
P = U . I
Cas d’un récepteur
purement résistif ( Cosj = 1 comme
pour un convecteur, un four électrique …)
La puissance
active se mesure avec un wattmètre
PUISSANCE REACTIVE
(Q)
La puissance
réactive est la puissance consommée par une bobine
pure (inductance) ou par un condensateur
Q = U . I . Sinj
Elle s’exprime en volt-ampères réactifs (VAR)
RELATION ENTRE LES
PUISSSANCES
Les 3 puissances
peuvent être représentées par un triangle rectangle
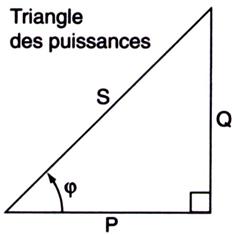
Dans ce triangle,
nous pouvons appliquer le théorème de Pythagore.
Et tirer les relations suivantes :
S = racine de P²+Q² P
= S .
Cosj Q = S . Sinj
Cosj = P/S
Sinj = Q/S
tgj = Q/P
COURANT
ALTERNATIF
Le courant
alternatif est produit industriellement par machines
tournantes appelées alternateurs
Comme son nom
l’indique, le courant alternatif va tantôt dans un sens, tantôt dans l’autre.

Alternance + Alternance - Période (T)
La courbe représentant
les variations du courant ou de la tension alternative est appelée sinusoïde
On dit qu’une telle tension est de forme sinusoïdale
Une
« vague » allant de zéro au maxi et revenant à zéro est une alternance.
Une alternance positive et une négative forment une période
Le nombre de périodes fournies en 1 seconde par un générateur alternatif est
appelé fréquence
En France il faut 20 ms à la
tension alternative pour effectuer une période
F = 1 / T
Pour connaître la fréquence
en Hertz (Hz) il faut appliquer la formule :
En France la fréquence est de :
F = 1/0,02
s = 50 Hz
DEPHASAGE
Lorsqu’une résistance est branchée sur un réseau alternatif, la tension et l’intensité varient simultanément. Leurs
effets sont conjugués

Toute l’énergie est utilisée.
Si une bobine est branchée sur un réseau alternatif, à
cause du champ magnétique provoqué par cette bobine l’intensité
est en retard sur la tension. Elles ne sont plus en phase : il y a
déphasage
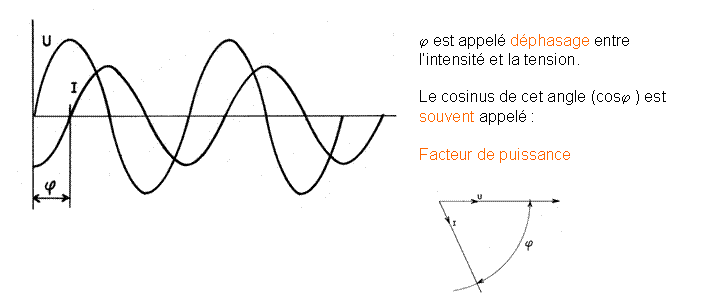
Les effets de la
tension et de l’intensité ne sont plus conjugués, la puissance apparente demandée au réseau est supérieure
à celle nécessaire au travail de la
bobine.
Il y a perte d’énergie
.
RESISTANCE,
REACTANCE et IMPEDANCE
-1- Résistance pure (exemple : convecteur,
four)
R = U/I
Sa résistance
est : Avec
R en ohm (W)
-2- Self pure ou Inductance (exemple : bobines
de mesures de courant d’un DDR – leur résistance est négligeable)
X = U/I X = L.w
Sa réactance
est
Avec L : inductance en Henrys (H)
Avec
w : pulsation
en radians par secondes : w=2pF
(F étant la fréquence en Hz)
-3- Résistance et inductance en série ou
Résistance inductive (exemple :
bobines de contacteur, de sonnette, de moteur…
)
Z = U/I Z = racine de
R² + L² w²

Son Impédance est
On peut aussi écrire :
L = racine
de Z²-R²/w cos j = R/Z
-4- Mesure de l’impédance
et de la résistance d’une bobine par la méthode de JOUBERT :
L’impédance Z dépend de la pulsation w =
2 p F, si on
s’arrange pour que w = 0
Z = racine de
R² Z = R
On pourra écrire : on
aura donc mesuré la résistance de la bobine

Méthode : en alimentant la bobine
en courant continu F = 0 donc w =
0
On mesure U et I et on écrit :
R =
U/I
Ensuite, si on recommence cette même mesure mais en courant alternatif

On ne mesure plus R mais Z
…………………………………………………………………………………
…………………………………………………………………………………
On mesure U et I et on écrit :
Z =
U/I
On pourra, ensuite, calculer l’inductance de cette bobine :
L = racine de Z²-R²/w avec w = 2.p.F
si
F = 50Hz , w = 2.p.50
Nota : on suppose que la résistance de
la bobine reste la même en continu et en alternatif

-5- Impédance d’un CONDENSATEUR
![]()
Un condensateur est formé de 2 armatures
![]()
conductrices séparées par un isolant appelé
diélectrique.
Cet isolant peut être solide, liquide ou gazeux
………………………………………………………………………………….


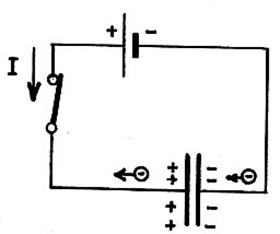
Lorsqu’un condensateur est branché sur un
générateur continu pendant quelques instants
il va se charger.….
………………………………………………………………………………….
Ses armatures sont électrisées, mais il n’y a pas
de passage du courant entre celles-ci.….
………………………………………………………………………………….
………………………………………………………………………………….
………………………………………………………………………………….

Lorsqu’un condensateur chargé est raccordé à un
récepteur, il devient générateur et se décharge.
Les électrons de l’armature négative vont vers les
Trous de l’armature positive pour rétablir l’équilibre.
La quantité d’électricité que peut charger un condensateur dépend de
L’unité de CAPACITE est le Farad (F)
mais comme c’est une unité très grande, on préfére
utiliser le sous-multiple :
Le micro
Farad
( mF)
Cette CAPACITE est :
- proportionnelle à la surface des armatures
-
inversement proportionnelle à la distance qui les sépare
- fonction de la nature du diélectrique
Impédance
d’un condensateur
La résistance interne d’un condensateur est considérée comme nulle R = 0 W
La réactance d’un condensateur est : X
= 1/Cw


si R = 0, le triangle de Joubert
devient :
Z = 1/Cw
L’Impédance sera :
Remarque :
UTILISATION
du condensateur :
Grâce à sa particularité de se charger et de se décharger, on l’utile en redressement pour LISSER la tension
Ce temps de charge et de décharge étant plus ou moins long suivant sa
capacité, on l’utilise pour réaliser des temporisations
ou minuteries.
……………………………………………………………………………………………………………………………………………………………
Grâce à sa particularité de déphaser de -90° le courant par rapport à la
tension, on l’utilise pour déphaser des circuits
(déphasage de la bobine de démarrage d’un moteur monophasé) ou pour redresser
le cosj d’une installation.
On appelle cela :
Amélioration
du facteur de puissance
1- Conséquence d’un mauvais facteur de
puissance :
Un mauvais facteur
de puissance entraîne un courant en ligne plus important
pour une puissance active identique (S augmente)
Un courant en
ligne plus important oblige :
-
A surdimensionner l’appareillage électrique en amont
-
A surdimensionner les lignes électriques
-
Crée des échauffements donc des chutes de tensions en ligne
-
Entraîne un coût de l’énergie plus élevé
Remarque : EDF pénalise l’industriel
dont l’installation présente un facteur de puissance inférieur à 0,93 en lui
facturant la puissance réactive consommée.
Les installations
industrielles principalement constituées
de récepteurs inductifs ( moteur, transformateur
éclairage fluorescent) sont consommateur d’énergie réactive Il est donc nécessaire de relever le facteur de puissance afin de limiter ces
inconvénients.
Or, si un récepteur inductif pur a un déphasage
de + 90° et donc consomme
de l’énergie réactive, un condensateur a un déphasage de
-90
° et donc produit de l’énergie réactive
Nous pouvons donc utiliser le condensateur
pour relever le cos j appelé aussi facteur de puissance.
-2 AMELIORATION DU FACTEUR DE PUISSANCE
par


Lorsqu’on ajoute
un condensateur en dérivation à une installation :
-
La puissance active P reste inchangée
- La puissance réactive Qc fournit par le condensateur
diminue la puissance réactive absorbée par l’installation.
La nouvelle
puissance réactive s’écrit : Q2 = Q1 - Qc.
Sachant que Q = P tang j
Il suffit de
choisir l’angle j2 pour pouvoir calculer
Qc :
Qc =
P tang j1 – P tang j2 = P (tang j1 – tang j2)
Puis pour calculer
la capacité du condensateur , prendre la 2eme formule de Qc :
Qc =U I
sin j = U I sin -90°
Avec I = U/Zc = U. Cw
QC =U² . Cw
. -1
D’où on
tire :
C = Qc/U².w. (on ne tient pas compte du -1)
>>>>
Retour à la page d’accueil